JParser (4) Naive 파싱 알고리즘

이번 포스팅에서는 CDG를 파싱할 수 있는 알고리즘을 설명해 보겠다. 이 알고리즘은 내가 naive 알고리즘이라고 부르고 있는데, 최적화에 대한 고민같은 것 없이 그냥 돌아가게 만드는데 목적을 맞추고 개발했던 알고리즘이라서 그렇게 이름을 붙였다. 뒤에서 문법에 대한 전처리를 거쳐 이보다 빠르게 파싱을 수행할 수 있는 알고리즘들에 대해서도 소개할 것이다.

이 알고리즘은 동작 방식상 Earley 파싱 알고리즘과 유사한데, 거기에 승인 조건(accept condition)이라는 개념이 추가된다. 처음 내가 이 파싱 알고리즘을 개발하기 시작했을 땐 Earley 파싱 알고리즘에 대해서 모르고 있었는데, 알고리즘을 다 개발하고 나서 논문을 써보려고 공부를 하다 이 알고리즘의 존재를 알게 되었다. 혹시 Earley 파싱에 대해 알고있는 사람이라면 이 포스팅의 내용을 조금 더 이해하기 쉬울 지도 모르겠다.

알고리즘은 수학적인 언어를 사용하기보다는 실제 구현된 코드를 인용하면서 설명하고자 한다. 수학적인 설명은 부록으로 다루어 보겠다.

Parser Studio

본격적으로 알고리즘을 설명하기 전에, 실제로 CDG와 이 파싱 알고리즘을 실험해보고 시각적으로 확인해볼 수 있는 방법을 소개한다. JParser에는 Parser studio라는 기능이 지원된다.

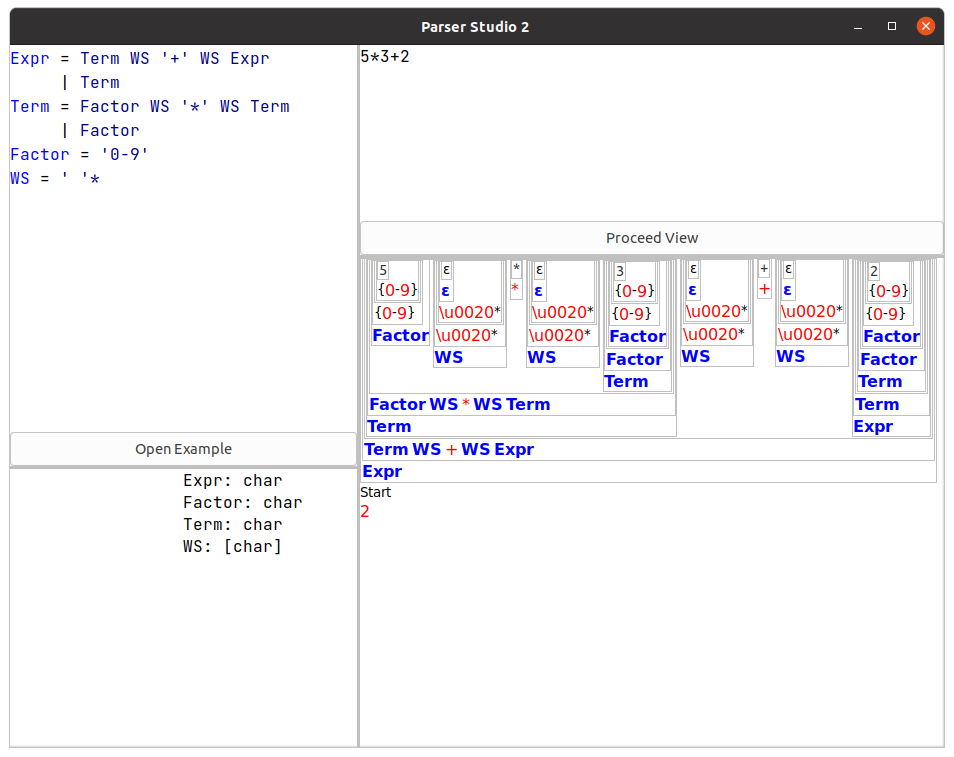
Parser studio

왼쪽 위에 문법을 CDG 포맷으로 입력하고, 오른쪽 위에 테스트해볼 문자열을 입력하면 오른쪽 하단에 파스 트리가 표시된다. 그 밑부분과 (위의 스크린샷에 빨간 글씨로 “2”라고 표시된 부분) 왼쪽 하단은 AST 기능과 관련된 내용인데, 이 부분은 추후에 다루기로 하자. 여기서 “Proceed View” 버튼을 누르면 아래서 다룰 “파싱 컨텍스트”를 시각화해서 볼 수 있다.

이 프로그램을 실행시키려면 JParser 소스코드를 다운로드 받고, 최신 버전의 bibix를 다운로드 받아 jparser 디렉토리에 넣은 다음 그 디렉토리에서 java -jar bibix-0.0.4.jar parserStudio2 라는 커맨드를 실행하면 된다.

처음에는 sbt로 빌드 스크립트가 만들어져 있었고, 지금도 build.sbt 파일이 있긴 하다. 그런데 하다보니 코드 구조가 꼬여서 지금은 sbt로는 빌드가 되지 않는다.

한가지 아쉬운 점은 이 시각화 기능을 내가 SWT로 만들어서 플랫폼간 호환이 잘 되지 않는다는 점이다. 그래서 지금은 리눅스 GTK 환경에서만 실행해볼 수 있다. 빌드 스크립트에 SWT 의존성만 살짝 바꾸면 실행이 되긴 할 것이다. 지금 Swing으로 다시 만드는 작업을 하고 있긴 한데 우선순위를 높게 잡고 있지 않은 탓에 작업 속도가 늦어서 언제 완성될 지는 알 수 없다.

심볼

CDG는 RHS에 터미널과 넌터미널의 시퀀스만 들어갈 수 있는 것이 아니라, <A>나 A-B같은 확장 심볼, A?라든가 A* 같은 편의 심볼이나, (A B)*와 같은 nested sequence도 들어갈 수 있다. (물론 CDG에서도 룰의 LHS에는 넌터미널만 들어갈 수 있다) 그래서 CDG에서 ‘심볼’은 터미널과 넌터미널 외에도 다음과 같은 여러 종류가 있다.

실제 jparser 코드에서는 CDG 심볼들을 나타내기 위한 클래스들이 Symbols.scala 파일에 다음과 같이 정의되어 있다.

sealed trait Symbol

sealed trait AtomicSymbol extends Symbol

sealed trait Terminal extends AtomicSymbol { ... }

case object Start extends AtomicSymbol

case class Nonterminal(name: String) extends AtomicSymbol { ... }

case class Sequence(seq: Seq[AtomicSymbol]) extends Symbol { ... }

case class Proxy(sym: Symbol) extends AtomicSymbol { ... }

case class OneOf(syms: ListSet[AtomicSymbol]) extends AtomicSymbol { ... }

case class Repeat(sym: AtomicSymbol, lower: Int) extends AtomicSymbol { ... }

sealed trait Lookahead extends AtomicSymbol

case class LookaheadIs(lookahead: AtomicSymbol) extends Lookahead { ... }

case class LookaheadExcept(except: AtomicSymbol) extends Lookahead { ... }

case class Except(sym: AtomicSymbol, except: AtomicSymbol) extends AtomicSymbol { ... }

case class Join(sym: AtomicSymbol, join: AtomicSymbol) extends AtomicSymbol { ... }

case class Longest(sym: AtomicSymbol) extends AtomicSymbol { ... }

위에서 설명하지 않은 Start라는 object는 시작 심볼을 RHS로 갖는 가상의 심볼로, 실제 시작 넌터미널을 derive하는 심볼이다. 이 심볼을 도입하면 구현이 조금 더 간단해진다.

위의 심볼들을 사용해서 코드상에서 문법은 다음과 같이 정의된다. (Grammar.scala)

trait Grammar {
  type RuleMap = ListMap[String, List[Symbols.Symbol]]

  type Symbol = Symbols.Symbol

  val name: String
  val rules: RuleMap
  val startSymbol: Symbols.Nonterminal
}

다만 파싱 알고리즘의 구현상에서 심볼과 심볼이 같은지를 비교하는 경우가 많은데, 위와 같이 심볼들을 정의하면 심볼 비교가 더 느려진다고 생각해서 NSymbol이라는걸 만들었다. NGrammar.scala

sealed trait NSymbol {
  val id: Int
  val symbol: Symbols.Symbol
}

sealed trait NAtomicSymbol extends NSymbol {
  override val symbol: Symbols.AtomicSymbol
}

case class NTerminal(id: Int, symbol: Symbols.Terminal) extends NAtomicSymbol

sealed trait NSimpleDerive { val produces: Set[Int] }

case class NStart(id: Int, produce: Int) extends NAtomicSymbol with NSimpleDerive {
  val symbol: Symbols.Start.type = Symbols.Start
  val produces: Set[Int] = Set(produce)
}

case class NNonterminal(id: Int, symbol: Symbols.Nonterminal, produces: Set[Int])
    extends NAtomicSymbol with NSimpleDerive

case class NOneOf(id: Int, symbol: Symbols.OneOf, produces: Set[Int])
    extends NAtomicSymbol with NSimpleDerive

case class NProxy(id: Int, symbol: Symbols.Proxy, produce: Int)
    extends NAtomicSymbol with NSimpleDerive {
  val produces: Set[Int] = Set(produce)
}

case class NRepeat(id: Int, symbol: Symbols.Repeat, baseSeq: Int, repeatSeq: Int)
    extends NAtomicSymbol with NSimpleDerive {
  val produces: Set[Int] = Set(baseSeq, repeatSeq)
}

case class NExcept(id: Int, symbol: Symbols.Except, body: Int, except: Int) extends NAtomicSymbol

case class NJoin(id: Int, symbol: Symbols.Join, body: Int, join: Int) extends NAtomicSymbol

case class NLongest(id: Int, symbol: Symbols.Longest, body: Int) extends NAtomicSymbol

sealed trait NLookaheadSymbol extends NAtomicSymbol {
  val symbol: Symbols.Lookahead
  val emptySeqId: Int
  val lookahead: Int
}

case class NLookaheadIs(id: Int, symbol: Symbols.LookaheadIs, emptySeqId: Int, lookahead: Int)
    extends NLookaheadSymbol

case class NLookaheadExcept(id: Int, symbol: Symbols.LookaheadExcept, emptySeqId: Int, lookahead: Int)
    extends NLookaheadSymbol

case class NSequence(id: Int, symbol: Symbols.Sequence, sequence: Seq[Int]) extends NSymbol

이 NSymbol들을 받는 NGrammar도 있다. NGrammar.scala

class NGrammar(
  val nsymbols: Map[Int, NGrammar.NAtomicSymbol],
  val nsequences: Map[Int, NGrammar.NSequence],
  val startSymbol: Int) {
  ...
}

구현상에서는 Grammar 객체를 받으면, NGrammar로 변환(NGrammar.fromGrammar)해서 파싱시에는 NGrammar를 사용한다.

그래서 파싱시에는 심볼의 내용 대신 심볼의 ID만 사용해서 심볼의 비교를 Int값 두 개 비교로 끝낼 수 있도록 했다.

평이한 CDG

앞으로 확장 심볼을 사용하지 않는 CDG는 평이한(Plain) CDG라고 부를 것이다. 평이한 CDG는 CFG로도 동일한 언어를 표현할 수 있다.

파싱 컨텍스트(Parsing context)

CDG 파싱 알고리즘은 파싱 컨텍스트로부터 시작한다. 파싱 컨텍스트는 실제 파싱을 시작하기 전에 먼저 초기 상태가 만들어지고, 입력 스트링의 글자들을 맨 앞에서부터 한 글자씩 처리하면서 업데이트된다. 우리는 초기 상태의 파싱 컨텍스트를 generation 0 파싱 컨텍스트라고 부르고, 한 글자를 처리하면서 업데이트될 때마다 generation은 1씩 증가한다.

한 글자를 처리하고 나면 다시는 과거의 글자들을 볼 필요가 없고, 앞으로 올 글자들을 미리 살펴볼 필요도 없다. 다만 파싱이 끝나고 나서 파스 트리를 구성하려면 각 단계의 파싱 컨텍스트를 모두 기록해 두어야한다. 엄밀히 말하면 파싱은 입력 스트링이 문법에 맞는지 아닌지를 true/false로 반환하는 작업이고, 파스 트리를 구성하는건 별도의 작업이기 때문에 “파싱”만을 위해선 각 시점의 파싱 컨텍스트만 알고 있고 한 글자씩 처리해나가면 된다.

파싱 컨텍스트는 그래프로써, 그래프의 노드는 커널(kernel)과 승인 조건(accept condition)의 페어(pair; 값이 2개인 튜플)이다. 커널은 (심볼, 포인터, 시작 위치, 종료 위치)의 4-튜플이다. 즉, 파싱 컨텍스트의 노드는 ((심볼, 포인터, 시작 위치, 종료 위치), 승인 조건)의 형태를 갖는다. 승인 조건은 일종의 수식이라고 볼 수 있는데, 평이하지 않은 문법, 즉 확장 심볼을 포함한 문법을 처리할 때 사용한다. 승인 조건에 대해서는 다음 포스팅에서 자세히 알아보기로 하고 이번 포스팅에서는 신경쓰지 않고 커널부터 이야기해보자.

Atomic 심볼(sequence를 제외한 모든 심볼) 커널의 포인터는 0이거나 1이고, 길이가 n인 시퀀스 심볼 커널의 포인터는 0과 n 사이의 정수이다. 포인터가 1인 atomic 심볼의 노드나 시퀀스의 길이와 포인터가 동일한 시퀀스 심볼의 노드는 “종료되었다”고 한다.

Generation g의 파싱 컨텍스트에 atomic 심볼 A에 대한 ((A, 0, s, s), ∅)라는 노드가 들어있는 것은, 인풋 스트링 source에 대해 source[s:g+k] (k > 0)에 A라는 심볼이 매칭될 가능성이 있어서 현재 추적중임을 의미한다. Generation X의 파싱 컨텍스트에 시퀀스 심볼 $Q$에 대한 (종료되지 않은) 노드 ((Q, p, s, e), ∅)가 있다는 것은, Q[:p]가 source[s:e] 사이에서 이미 매칭되었고, Q[p]에 해당하는 심볼이 source[e:g+k] (k > 0) 이후로 매칭될 가능성이 있어 현재 추적중임을 의미한다. (스트링 인덱스는 파이썬식으로 start는 inclusive, end는 exclusive하게 표현하였다)

Atomic 심볼의 노드 X에서 노드 Y로 가는 엣지가 있다는 것은, Y가 종료되면 X도 종료될 수 있음을 의미한다. Sequence 심볼 $Q$에 대한 (종료되지 않은) 노드 $X=((Q, p, s, e), ∅)$에서 Y로 가는 엣지가 있으면 Y는 Q[p]에 대한 노드이다. Sequence 심볼의 엘리먼트는 모두 atomic 심볼이어야 하므로 Y는 atomic 심볼의 노드일 것이다. X에서 Y로 가는 엣지가 있으면 Y가 종료되면 X가 progress될 수 있음을 의미한다. X가 progress된다는 것은 X에서 포인터와 종료 위치가 업데이트된 새로운 노드를 추가함을 의미한다.

코드상에서는 파싱 컨텍스트는 다음과 같이 정의되어 있다. (ParsingContext.scala)

case class Kernel(symbolId: Int, pointer: Int, beginGen: Int, endGen: Int) { ... }

case class Node(kernel: Kernel, condition: AcceptCondition) { ... }

case class Edge(start: Node, end: Node) extends AbstractEdge[Node] { ... }

case class Graph(
  nodes: Set[Node],
  edges: Set[Edge],
  edgesByStart: Map[Node, Set[Edge]],
  edgesByEnd: Map[Node, Set[Edge]]
) extends AbstractGraph[Node, Edge, Graph] { ... }

Kernel 클래스의 symbolId는 NSymbol의 ID, pointer는 커널의 포인터를, beginGen과 endGen은 각각 시작 genration과 종료 generation을 나타낸다.

위에서 설명한 구조를 그대로 반영하고 있다. Graph에 있는 edgesByStart, edgesByEnd나 AbstractGraph는 그냥 구현을 편리하고 동작 속도를 조금 더 개선하기 위해 추가된 것이므로 동작에 영향을 주지는 않는다.

다음의 문법을 보자.

Expr = Term WS '+' WS Expr
     | Term
Term = Factor WS '*' WS Term
     | Factor
Factor = '0-9'
     | '(' WS Expr WS ')'
WS = ' '*

+와 * 연산자를 지원하는 이 간단한 문법의 초기 파싱 컨텍스트는 다음과 같다.

그래프

그래프 1: 초기 상태의 파싱 컨텍스트 예제. 보다 간결하게 표현하기 위해 그래프에는 커널의 포인터가 커널의 심볼 사이에 점으로 표시되어 있고, 시작 위치와 종료 위치가 ..으로 연결되어 표시되어 있다. 즉, (Start, 0, 0, 0)은 (•Start, 0..0)으로 표시된다. ∅으로 표현된 승인 조건 부분은 다음 포스팅에서 자세히 이야기하고 여기서는 잠시 무시하고 넘어가자.

이 그래프를 자세히 살펴보자. (• Expr, 0..0) 노드가 이 파싱 컨텍스트에 있다는 것은 generation 0 이후로 Expr 심볼이 매칭될 가능성이 있음을 나타낸다. 그리고 이 노드에서 두 개의 엣지가 나오는데, 하나는 ((• Term WS '+' WS Expr, 0..0), ∅) 노드로 가고 하나는 ((• Term, 0..0), ∅) 노드로 간다. 이건 문법 정의에서 Expr 넌터미널의 RHS가 두 개가 있기 때문에 하나의 RHS에 대해 두개가 생긴 것이다. 그리고 이 두 노드는 모두 ((• Term, 0..0), ∅) 노드로 가는데, 이건 두 노드 모두 포인터 뒤에 나오는 심볼이 Term이기 때문이다.

만약 파싱이 진행되면서 다음 글자가 ‘1’이었고, 그래서 다음 generation 1에서 Term 심볼이 매칭된다면, ((• Term, 0..0), ∅) 노드는 종료될 것이고, 연쇄적으로 (• Expr, 0..0)도 종료될 것이다. 하지만 동시에 Term 심볼이 매칭되면 ((• Term WS '+' WS Expr, 0..0), ∅)는 종료되지는 않고 progress 되면서 ((Term • WS '+' WS Expr, 0..0), ∅) 노드가 생기면서 기존의 (• Expr, 0..0) 노드에서 새로운 노드로 가는 엣지가 추가된다. 이는, source[0:1]=”1”로 인해 Term 심볼이 매칭되면, 그로 인해 source[0:1]은 Expr 심볼에도 매칭될 수 있고, 그래서 source가 [0:1]에서 끝나도 정상적으로 파싱이 종료됨을 의미한다. 하지만 generation 1에도 여전히 Start 심볼의 노드가 남아있고, Start 심볼에서 나오는 ((Term • WS '+' WS Expr, 0..0), ∅) 노드가 살아있기 때문에, 다른 형태로 파싱이 추가 진행될 가능성이 남아있음을 의미한다.

처음부터 이걸 다 이해할 필요는 없고.. 뒤의 상세 내용을 보다 보면 좀 더 이해가 될 것이다. 사실 내가 만든 알고리즘인데도 나도 항상 조금 헷갈리기 때문에..

파싱 태스크

파싱 컨텍스트를 만들땐 세가지 종류의 “파싱 태스크”를 사용한다. 초기 파싱 컨텍스트를 만들때나 한 글자를 처리하면서 업데이트될 때나 기본 원리는 거의 동일하다. 파싱 태스크에는 Derive, Progress, Finish 세가지 종류가 있다. Derive 태스크는 새로운 노드가 파싱 컨텍스트에 추가될 때마다 생성된다. Finish 태스크는 어떤 노드가 종료되면 생성되고, 종료된 노드로 들어오는 엣지의 반대편에 있는 노드들에 대해 Progress 태스크가 생성된다. 앞에서는 atomic 심볼의 노드 X에서 Y로 가는 엣지가 있으면 “Y가 종료되면 X도 종료된다”라고 표현했는데, 실제로는 “Y가 종료되면 X가 progress되고, X는 atomic 심볼이므로 progress되면 이어서 finish된다”라는 표현이 더 정확할 것이다.

파싱 컨텍스트를 만들땐, 태스크 큐를 갖게 된다. 한 태스크가 실행되면 파싱 컨텍스트가 업데이트되거나 태스크 큐에 새로운 태스크가 추가되거나, 둘 다 일어난다. 초기 파싱 컨텍스트를 만들 땐 ((Start, 0, 0, 0), ∅)라는 노드가 파싱 컨텍스트에 추가되고 이 노드에 대한 Derive 태스크가 태스크 큐에 추가된다. 글자가 처리될 땐 다음에 오는 글자를 받을 수 있는 터미널 심볼에 대한 노드들에 대해 Progress 태스크를 만들어서 태스크 큐에 추가한다. 각 종류의 태스크에 대해 좀 더 자세히 알아본 다음 실제 사례를 살펴보자.

이 섹션의 코드는 ParsingTasks.scala 파일에 있다. 이 코드를 쓸 때 함수형 코드에 대한 집착같은게 좀 있던 시절이라 모든 데이터가 immutable하게 만들려다보니 코드가 읽기에 썩 좋지는 않다. 그리고 여기에 글로 정리하다보니 코드가 약간 이상한 부분들도 있다. 코드를 쓸 때는 알고리즘을 정확히 모르고 좌충우돌 고쳐가면서 만들었기 때문에 그 흔적이 남아있다고 할까.. 나중에 언젠가 정리할 날이 올 지는 모르겠지만 일단은 설명에 집중해보자.

Derive 태스크

Derive 태스크는 하나의 노드를 인자로 포함한다.

case class DeriveTask(node: Node) extends Task

Derive 태스크가 큐에 추가되면 deriveTask 함수가 실행된다.

def deriveTask(nextGen: Int, task: DeriveTask, cc: Cont): (Cont, Seq[Task]) = {
  val DeriveTask(startNode) = task

  assert(cc.graph.nodes contains startNode)
  assert(!startNode.kernel.isFinal(grammar))
  assert(startNode.kernel.endGen == nextGen)
  ...
}

deriveTask함수가 받는 nextGen은 이번에 생성중인 그래프가 몇 번째 generation인지 나타낸다. 즉, 처음에는 초기 파싱 컨텍스트를 만들 때는 이 값이 0으로 들어오고, 그 뒤에는 한 글자를 처리할 때마다 1씩 증가한다. Cont는 현재 생성중인 파싱 컨텍스트 그래프와 updatedNodesMap이라는 값의 페어이다. updatedNodesMap은 약간은 예외적인 경우를 처리하기 위해서 있는 것으로, 나중에 다시 이야기하기로 하자. 그래서 deriveTask 함수는 현재 생성중인 그래프인 cc, 이번에 생성중인 generation인 nextGen, 이번에 처리할 Derive 태스크를 받아서, 태스크를 수행하여 수정된 그래프와 새로 처리해야 할 태스크들의 리스트를 반환한다.

Derive 태스크로 오는 node는 아직 종료되지 않은 것이어야 하고, Derive 태스크는 지금 생성중인 그래프에 새로 추가된 노드에 대해서만 실행되어야 하므로 startNode.kernel.endGen == nextGen의 조건을 만족해야 한다.

지금 코드를 짠다면 Seq[Task] 부분은 어떤 식으로든 함수의 멤버 변수로 빼던가 Cont에 합치던가 해서 리턴 타입을 튜플로 만들지 않았을 것 같지만 이제와서 지금은 코드의 아쉬운 부분까지 고칠 힘이 없으니 넘어가기로 하자.

이 함수의 동작은 node의 심볼에 따라 달라진다.

val GraphTasksCont(newGraph, newTasks) = grammar.symbolOf(startNode.kernel.symbolId) match {
  case symbol: NAtomicSymbol =>
    symbol match {
      ...
    }
  case NSequence(_, _, seq) => ...
}

case symbol: NAtomicSymbol => symbol match {
  case _: NTerminal => gtc0 // nothing to do
  ...
}

case symbol: NAtomicSymbol => symbol match {
  ...
  case simpleDerives: NSimpleDerive =>
    simpleDerives.produces.foldLeft(gtc0) { (cc, deriveSymbolId) => derive0(cc, deriveSymbolId) }
  ...
}

case symbol: NAtomicSymbol => symbol match {
  ...
  case NExcept(_, _, body, except) =>
    addNode(derive0(gtc0, body), nodeOf(except))
  case NJoin(_, _, body, join) =>
    addNode(derive0(gtc0, body), nodeOf(join))
  case NLongest(_, _, body) =>
    derive0(gtc0, body)
  case lookaheadSymbol: NLookaheadSymbol =>
    addNode(derive0(gtc0, lookaheadSymbol.emptySeqId), nodeOf(lookaheadSymbol.lookahead))
}

case NSequence(_, _, seq) =>
  assert(seq.nonEmpty) // empty인 sequence는 derive시점에 모두 처리되어야 함
  assert(startNode.kernel.pointer < seq.length) // node의 pointer는 sequence의 length보다 작아야 함
  derive0(gtc0, seq(startNode.kernel.pointer))

위에서 인용한 코드에 nodeOf, addNode, derive0라는 함수가 나온다.

nodeOf 함수는 deriveTask 함수 안에 네스티드 함수로 정의되어 있는데, 단순하게 새로운 노드 클래스를 만든다.

def nodeOf(symbolId: Int): Node = Node(Kernel(symbolId, 0, nextGen, nextGen), Always)

Always는 가장 기본적인 승인 조건의 클래스로, 특별한 조건이 붙지 않았음을 의미한다. 자세한 이야기는 다음 포스팅에서 더 풀어보자.

addNode 함수는 말 그대로 그래프에 새로운 노드를 추가하는 함수다.

private def addNode(cc: GraphTasksCont, newNode: Node): GraphTasksCont =
  if (!(cc.graph.nodes contains newNode)) {
    // 새로운 노드이면 그래프에 추가하고 task도 추가
    val newNodeTask: Task =
      if (newNode.kernel.isFinal(grammar)) FinishTask(newNode) else DeriveTask(newNode)
    GraphTasksCont(cc.graph.addNode(newNode), newNodeTask +: cc.newTasks)
  } else {
    // 이미 있는 노드이면 아무 일도 하지 않음
    cc
  }

이 코드에서 눈여겨봐야할 것은 새로 추가하려는 노드가 종료된 경우(newNode.kernel.isFinal(grammar))에는 DeriveTask 대신 FinishTask를 만든다는 점이다. 앞서 Derive 태스크는 종료된 커널의 노드에 대해서는 만들어져서는 안된다고 했기 때문이다. 문법에 nullable 심볼이 있는 경우 이런 현상이 발생할 것이다.

derive0 함수는 deriveTask 함수 안에 네스티드 함수로 정의되어 있다.

def derive0(cc: GraphTasksCont, symbolId: Int): GraphTasksCont = {
  val newNode = nodeOf(symbolId)
  if (!(cc.graph.nodes contains newNode)) {
    // Case 1. newNode가 그래프에 없어서 새로 추가하는 경우
    val ncc = addNode(cc, newNode)
    GraphTasksCont(ncc.graph.addEdge(Edge(startNode, newNode)), ncc.newTasks)
  } else if (newNode.kernel.isFinal(grammar)) {
    // Case 2. newNode가 그래프에 이미 있고 newNode가 종료된 커널의 노드인 경우
    GraphTasksCont(
      cc.graph.addEdge(Edge(startNode, newNode)),
      ProgressTask(startNode, Always) +: cc.newTasks)
  } else {
    // Case 3. newNode가 그래프에 이미 있고 newNode가 종료되지 않은 커널의 노드인 경우
    assert(newNode.isInitial)
    val updatedNodes = updatedNodesMap.getOrElse(newNode, Set())
    val updatedFinalNodes = updatedNodes filter { _.kernel.isFinal(grammar) }
    // TODO: final node만 저장하도록 수정, assert(updatedFinalNodes forall { _.kernel.isFinal })
    val newTasks = updatedFinalNodes map { finalNode =>
      ProgressTask(startNode, finalNode.condition)
    }

    assert(!(updatedNodes contains newNode))
    val graph1 = cc.graph.addEdge(Edge(startNode, newNode))
    val newGraph = updatedNodes.foldLeft(graph1) { (graph, updatedNode) =>
      graph.addEdge(Edge(startNode, updatedNode))
    }
    GraphTasksCont(newGraph, newTasks ++: cc.newTasks)
  }
}

if else가 삼중으로 겹쳐져 있다. 가장 위의 조건(Case 1)은 새로 추가하려는 노드(nodeOf함수로 만든 newNode)가 cc의 그래프에 없는 경우이다. 이런 경우엔 새로운 노드를 그래프에 추가하고 Derive 태스크의 node인 startNode에서 새로운 노드로 가는 엣지를 추가하고 끝난다.

두번째 조건(Case 2)과 세번째 조건(Case 3)은 newNode가 이미 그래프에 있는 경우를 처리한다. 두번째 조건은 newNode가 종료된 경우로, startNode에서 endNode로 가는 엣지를 추가하고 startNode에 대한 Progress 태스크를 추가하고 끝난다. 이는 endNode가 이미 종료된 경우 endNode에 대한 Finish 태스크가 실행되고, 연쇄적으로 startNode에 대한 Progress 태스크가 실행되는데, endNode가 이미 그래프에 있다는 것은 endNode에 대한 Finish 태스크가 이미 실행되었다는 뜻이므로 다른 과정은 굳이 반복하지 말고 startNode에 대한 Progress 태스크를 실행하도록 하는 것이다.

세번째 조건은 조금 복잡하게 보이지만 사실 알고리즘을 이해하는데 크게 중요한 부분은 아니다. 쉽게 말해서 태스크가 실행되는 순서에 따라 만들어지는 그래프가 달라질 수 있는 부분을 보정하기 위한 것인데, 뒤에서 다시 설명해보도록 하겠다.

Progress 태스크

Progress 태스크는 하나의 노드와 하나의 승인 조건을 인자로 받는다.

case class ProgressTask(node: Node, condition: AcceptCondition) extends Task

Progress 태스크도 Derive 태스크와 마찬가지로 progressTask라는 함수가 처리하고, 이 함수의 시그니쳐는 deriveTask와 동일하다.

def progressTask(nextGen: Int, task: ProgressTask, cc: Cont): (Cont, Seq[Task]) = {
  val ProgressTask(node, incomingCondition) = task

  assert(!node.kernel.isFinal(grammar))
  assert(cc.graph.nodes contains node)
  ...
}

Progress 태스크가 하는 일은 간단하게 말하면 node에서 커널의 포인터가 1 증가한 노드를 만들어서 그래프에 추가하는 일이다. Progress 태스크가 실행되는 가장 전형적인 상황은 새로운 글자를 입력 받아서 다음 generation의 파싱 컨텍스트를 만드는 경우이다. 이런 경우 새로운 글자와 일치하는 terminal 심볼의 커널을 갖는 노드들에 대해 Progress 태스크를 실행하게 된다.

그래서 다음의 코드와 같이 새로 추가할 노드를 만들게 되고, 여기서 가장 중요한 부분은 커널의 포인터를 1 증가시키는 부분(kernel.pointer + 1)이다.

val kernel = node.kernel
val newKernel = Kernel(kernel.symbolId, kernel.pointer + 1, kernel.beginGen, nextGen)
val updatedNode = Node(newKernel, conjunct(node.condition, incomingCondition, newCondition))

그리고 그렇게 만들어진 updatedNode를 그래프에 추가한다. 이 때, Progress 태스크의 node로 들어오는 엣지들에서 updatedNode로 가는 엣지들도 함께 추가해준다. addNode 함수에 의해 새로운 노드가 종료된 노드이면 Finish 태스크를, 아니면 Derive 태스크도 만들어서 태스크 큐에 추가된다.

val GraphTasksCont(graph1, newTasks) = addNode(GraphTasksCont(cc.graph, List()), updatedNode)

// node로 들어오는 incoming edge 각각에 대해 newNode를 향하는 엣지를 추가한다
val incomingEdges = cc.graph.edgesByEnd(node)
val newGraph = incomingEdges.foldLeft(graph1) { (graph, edge) =>
  val newEdge = Edge(edge.start, updatedNode)
  graph.addEdge(newEdge)
}

이어서 Cont의 updatedNodesMap도 업데이트해 주는데, 앞서 Derive 태스크에서 이 값이 사용되는 것을 보았다. 이 값의 진짜 의미는 뒤에서 다시 이야기하기로 하자.

// cc에 updatedNodes에 node -> updatedNode 추가
val newUpdatedNodesMap = cc.updatedNodesMap +
  (node -> (cc.updatedNodesMap.getOrElse(node, Set()) + updatedNode))

(Cont(newGraph, newUpdatedNodesMap), newTasks)

자, 여기서 잠시 updatedNode의 승인 조건을 만드는 부분을 보자. 승인 조건은 Progress 태스크를 거치면서 누적되는 식으로 동작한다. 그래서 가장 기본은 Always라는 값으로, 승인 조건 Always는 해당 노드에는 아무런 승인 조건이 붙지 않았음을 의미한다. conjunct 함수는 이런 승인 조건들을 and 조건으로 연결시키는 함수로, 여러 개의 승인 조건들을 누적시키는 함수라고도 할 수 있겠다. Progress 태스크를 통해 전달되는 incomingCondition은 현재 노드에 대한 Progress 태스크를 유발한 노드의 승인 조건이고, newCondition은 현재 처리중인 node의 커널의 심볼이 확장 심볼인 경우 해당 심볼에 의해 추가되는 조건을 의미하는 것으로, 새로 생성되는 updatedNode에는 이들 조건을 모두 누적시킨 승인 조건이 설정된다. 자세한 이야기는 다음 포스팅에서 하기로 하자.

Finish 태스크

Finish 태스크도 Derive 태스크처럼 하나의 노드만 인자로 받고 deriveTask, progressTask와 동일한 시그니쳐를 갖는 finishTask 함수에서 처리된다.

case class FinishTask(node: Node) extends Task
def finishTask(nextGen: Int, task: FinishTask, cc: Cont): (Cont, Seq[Task]) = {
  ...
}

finishTask 함수는 앞서 다룬 두 함수에 비해 매우 간단해서 별다른 설명이 필요 없을 정도다.

def finishTask(nextGen: Int, task: FinishTask, cc: Cont): (Cont, Seq[Task]) = {
  val FinishTask(node) = task

  assert(cc.graph.nodes contains node)
  assert(node.kernel.isFinal(grammar))
  assert(node.kernel.endGen == nextGen)

  val incomingEdges = cc.graph.edgesByEnd(node)
  val chainTasks: Seq[Task] = incomingEdges.toSeq map { edge =>
      ProgressTask(edge.start, node.condition)
  }
  (cc, chainTasks)
}

코드에서 보이는대로, 그래프에는 변경이 없고 node로 들어오는 엣지들을 찾아서 해당 엣지의 시작 위치에 있는 노드들에 대한 Progress 태스크를 만들어 태스크 큐에 추가하는게 전부다. 이 때 생성되는 Progress 태스크들의 승인 조건 인자에는 node의 승인 조건이 들어간다.

전체적인 파싱 과정

위에서 설명한 세 가지의 태스크들은 다음과 같이 처리된다.

def process(nextGen: Int, task: Task, cc: Cont): (Cont, Seq[Task]) = task match {
  case task: DeriveTask => deriveTask(nextGen, task, cc)
  case task: ProgressTask => progressTask(nextGen, task, cc)
  case task: FinishTask => finishTask(nextGen, task, cc)
}

@tailrec final def rec(nextGen: Int, tasks: List[Task], cc: Cont): Cont = tasks match {
  case task +: rest =>
    val (ncc, newTasks) = process(nextGen, task, cc)
    rec(nextGen, newTasks ++: rest, ncc)
  case List() => cc
}

설명을 엄청나게 주절주절 해 놓았는데, 앞서 이야기한 DeriveTask, ProgressTask, FinishTask와 Graph라는 표현을 갖고 전체적인 파싱 과정을 간단히 설명하면 이렇게 된다. (NaiveParser.scala를 참고하되 이 아래의 코드는 실제 구현체 코드는 아니다)

먼저 초기 상태를 만들기 위해서는 Start 심볼에 대한 노드를 가진 그래프를 만들고, 그 노드에 대한 Derive 태스크를 태스크 큐에 넣고 rec 함수를 실행한다.

val startNode = Node(Kernel(grammar.startSymbol, 0, 0, 0), Always)
val initialGraph = Graph(nodes = Set(startNode), edges = Set())
val Cont(graph, _) = rec(0, List(DeriveTask(startNode)), initialGraph)

이렇게 해서 만들어진 graph가 초기 파싱 컨텍스트가 된다. Cont의 updatedNodesMap는 그래프를 만들고 나면 필요 없는 값이기 때문에 버린다.

이 다음 새로운 글자를 처리할 때는 파싱 컨텍스트의 터미널 심볼 노드들 중, pointer가 0이고, beginGen이 현재의 generation과 동일하며(pointer가 0이면 beginGen가 endGen이 동일해야 하므로 endGen도 현재 generation과 동일할 것이다), 새로운 글자를 처리할 수 있는 터미널 심볼인 것들을 묶어서 ProgressTask를 만든다. ProgressTask의 승인 조건은 Always로 한다. 코드로 쓰면 이렇다.

def proceed(parsingContext: Graph, nextInput: Char, nextGen: Int): Graph = {
  def terminalAcceptsInput(symbolId: Int): Boolean =
    // symbolId가 nextInput과 일치하는 터미널 심볼인 경우에만 true를 반환하고 그렇지 않으면 false를 반환한다.
    grammar.nsymbols(symbolId) match {
      case NTerminal(_, terminal) => terminal.accept(nextInput)
      case _ => false
    }

  val finishableTermNodes = parsingContext.nodes filter { node =>
    node.kernel.pointer == 0 &&
      node.kernel.beginGen == nextGen &&
      terminalAcceptsInput(node.kernel.symbolId)
  }
  if (finishableTermNodes.isEmpty) {
    // unexpected input이 들어왔다는 오류를 발생시킴
  } else {
    val progressTasks = finishableTermNodes map { ProgressTask(_, Always )}
    rec(nextGen, progressTasks, parsingContext).graph
  }
}

실제로는 초기 파싱 컨텍스트 만들기나 proceed에서 rec 함수를 실행한 뒤에 승인 조건을 위한 처리와 그래프 트리밍을 위한 처리가 추가된다.

태스크의 실행 순서

기본적으로 파싱 컨텍스트를 만들면서 수행되는 파싱 태스크의 실행 순서는 결과에 영향을 미치지 않아야 한다. 그런데 파싱 태스크의 실행 순서가 결과에 영향을 미칠 수가 있다. 다음의 문법을 보자.

A = B | C
B = D
C = D
D = ε | 'd'
E = 'e'

Derive((•A,0..0),∅) 태스크가 수행되면 ((•B,0..0),∅) 노드와 ((•C,0..0),∅) 노드가 추가되고, 이 새로운 노드들에 대한 Derive 태스크가 실행될 것이다. B 심볼의 노드에 대한 Derive가 먼저 실행되었다고 가정해보자. 그럼 ((•D,0..0),∅) 노드가 추가될 것이고, D는 nullable하기 때문에 D 노드에 대한 Progress 태스크가 수행되고, 연쇄적으로 B 심볼의 노드에 대해서도 Progress가 수행되고, 그 다음에 ((•C,0..0),∅) 노드에 대한 Derive 태스크가 실행되었다고 하자. ((•C,0..0),∅)는 ((•D,0..0),∅) 노드를 추가하려고 할텐데, D 심볼의 노드는 이미 추가되어 있으므로 C 노드에서 D 노드로 가는 엣지만 추가한다.

그런데 여기서 문제가 생긴다 D 심볼이 nullable하다는 점이다. D가 nullable하기 때문에 D 심볼의 노드에 대한 Derive가 수행되면 이어서 Progress가 수행되는데, 그 시점이 ((•C,0..0),∅) 노드에 대한 Derive가 수행되기 전이라는 점이다. 그러면 아직 C 심볼의 노드에서 D 심볼의 노드로 가는 엣지가 추가되기 전이고, D 심볼 노드의 Progress가 C 심볼의 노드로 전달되지 않는다.

앞서 deriveTask의 Case 3은 바로 이런 경우를 처리해주는 코드이다. progressTask 코드에서는 이런 경우를 위해 노드가 progress되어 업데이트된 기록, 즉 위의 예에서 ((•D,0..0),∅) 노드가 ((D•,0..0),∅)로 변모했던 것을 기록해둔다.

jparser에서는 동일한 태스크가 두 번 이상 만들어지거나 실행되지 않도록 하기 위해서 이렇게 구현되었는데, 이렇게 하는게 정 싫다면 필요할 때 태스크를 중복해서 실행하면 이런 코드를 없앨 수도 있을 것 같다.

그래프 트리밍

파싱이 진행되면서 파싱 컨텍스트에 완전히 불필요한 데이터가 남게될 수 있다. 예를 들어 Node(('a', 0, 0, 0), Always)와 Node(('b', 0, 0, 0), Always)라는 두 개의 터미널 심볼 노드가 있었을 때, 인풋 스트링의 첫번째 글자가 a였다면 'b' 터미널 심볼에 대한 노드는 generation 1에서부터는 필요가 없게 된다.

이런 데이터들은 지워주는 것이 파싱 속도에 유리하기 때문에 그래프에서 불필요한 내용은 쳐내는(trimming) 작업을 수행하는 것이다. NaiveParser.scala의 trimGraph 함수가 그 작업을 하는데, 특별한 내용은 없고 그냥 Start 심볼 노드에서 도달 가능하거나(승인 조건을 위한 고려를 포함해서) 다음 generation에 받을 수 있는 터미널 노드들로 도달 가능한 노드들을 제외하고 모두 제거하는 것이다.

전체 목차:

이 포스팅에서는 코드를 줄줄이 늘어놓고 있는 그대로 설명을 했기 때문에 이것만으로는 이해하기가 쉽지 않을 것이다. 다음 포스팅에서는 예제를 통해 이 알고리즘의 실제 동작 과정을 살펴 볼 것이다. 그리고 그 다음 포스팅에서는 승인 조건에 대한 이야기를 해보자.

이 페이지에서 오류나 문제점을 발견하시면 이메일로 알려주시면 감사하겠습니다.
뒤로